The Cryptopals challenge can be tricky based on how you approach it. Wanting to get to the details of particular tasks can be a daunting task.

Challenge 23 is one of those challenges. It seems easy to implement at first, but when you get to actual details, it’s not so easy. Especially for those of us who aren’t used to bitwise operations on a regular basis.

The challenge is to write an “untemper” function that takes an MT19937 output and transforms it back into the corresponding element of the MT19937 state array.

This is the “temper” code which we need to reverse:

1
2
3
4
5

y := m.data[m.index]
y1 := y ^ ((y >> _U) & _D)
y2 := y1 ^ ((y1 << _S) & _B)
y3 := y2 ^ ((y2 << _T) & _C)
o := y3 ^ (y3 >> _L)

So given o we should be able to obtain y while propagating through intermediary states (y1, y2, y3).

Lets take this one step at a time and break it down to obtaining each of those intermediary states.

y3 Link to heading

o is obtained from y3 and _L (18) as follows.

1

o := y3 ^ (y3 >> _L)

Easier to follow visually as shown below

We can see that the first _L bits of Y can be obtained by just taking the first _L bits of o. The 32 - _L bits of y3 can be obtained by doing an XOR of o » _L with o. This is because A ^ B = C implies A = B ^ C.

So we’ve got a way to obtain y3 from o and _L.

1

y3 := o ^ (o >> _L)

y2 Link to heading

Now that we have y3 we can move forward and obtain y2 from _T (15) and _C (0xEFC60000). Given the equation:

1

y3 := y2 ^ ((y2 << _T) & _C)

Which looks like

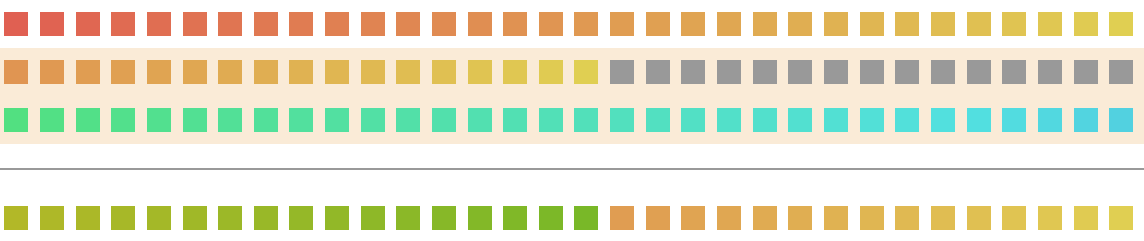
The last _T bits of y3 are the same as y2. This is because A & 0 = 0 and A ^ 0 = A. Which is visible from the diagram.

But this isn’t as simple as the previous step, is it? Yes and No.

No because you may have noticed that we only have 15 bits of untangled data (The last 15). So left shifting it with 15 would only give us the next 15 bits. Which is totally 30 bits out of 32 bits.

But Yes because, if you noticed _C, its first two bits are 11, which means that they don’t contribute to the output. We can think of this more clearly with the help of a diagram:

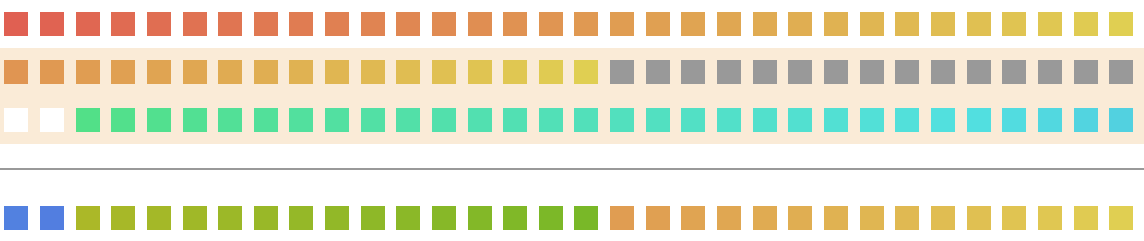
Notice:

• The first 2 bits only depend on y2
• The next 15 bits depend on y2, _C
• The last 15 bits are y2 itself This is now totally similar to the previous problem, we can now easily derive y2 from y3 by doing

1

y2 := y3 ^ ((y3 << _T) & _C)

y1 Link to heading

We’ve obtained y3, y2 now lets retrieve y1 from y2 given _S (7) and _B (0x9D2C5680).

1

y2 := y1 ^ ((y1 << _S) & _B)

Again, visualizing

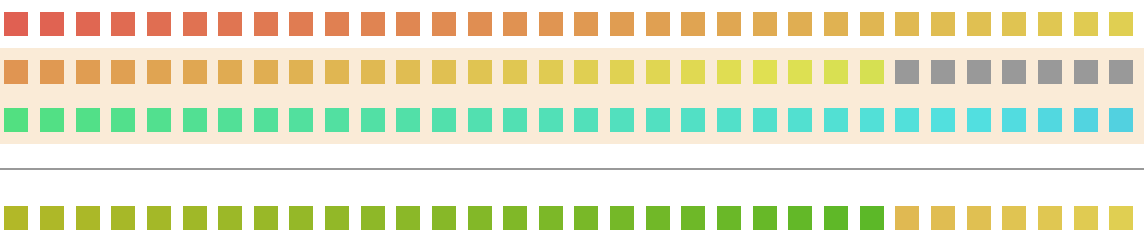
This is similar to the previous block, but there’s one big problem, we only have 7 bits of actual data. Going by the previous block this means that using this 7 bits we can generate only the next 7 bits of data.

Since we’re only generating 7 bits, we’d have to mask B so as to only use the parts of _B which actually effect in the calculation of the next 7 bits.

Let me explain visually:

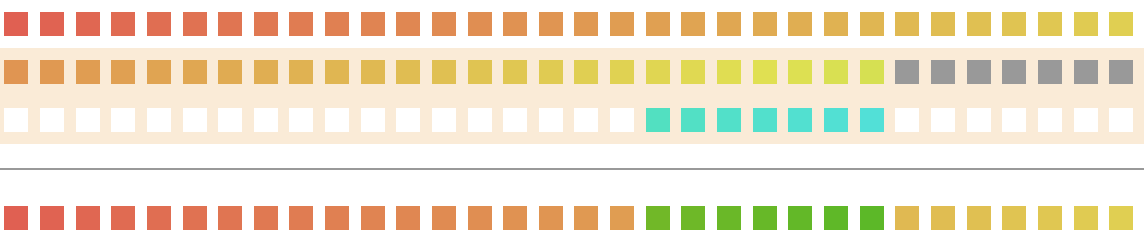
Therefore doing:

1
2
3

mask := 0x7f
b := _B & uint(mask << 7)
tmp1 := y2 ^ ((y2 << _S) & b)

would give us the following result, wherein the last 14 bits are of the original y1.

Now if you see the pattern, we can use this as the intermediate value and again do:

1
2

b := _B & uint(mask << 14)
tmp2 := tmp1 ^ ((tmp1 << _S) & b)

Which would now give us the next 7 bits as shown below:

Doing this two more times, we arrive with the final value:

Therefore the final result is just a loop with 4 iterations where we mask _B and do the same as the previous step. So the code for obtaining y1 from y2 is as follows.

1
2
3
4
5
6

y1 := y2
mask := 0x7f
for i := 0; i < 4; i++ {
	b := _B & uint32(mask << uint32(7 * (uint32(i) + 1)))
	y1 := y1 ^ ((y1 << _S) & b)
}

y Link to heading

This is the final value we need to obtain, with y1, y2, y3 in hand and _U (11) and _D (0xFFFFFFFF). Lets look at the equation to derive y1 from y. Which we need to reverse.

1

y1 := y ^ ((y >> _U) & _D)

Seems similar to the previous step, but anyone with a quick eye can see that _D is all 1s so potentially we can ignore it and shorten the equation to

1

y1 := y ^ (y >> _U)

Now lets visualize this

This is pretty similar to how we solved o <-> y3 but the only problem is that _U < 32 - _U. So we can use the same idea from the previous block. i.e. loop till we get the answer, since ( _U * 3 ) > 32. We’d need 3 loops.

Therefore, the solution is:

1
2
3
4

y := y1
for i := 0; i < 3; i++ {
	y1 := y1 ^ (y1 >> _U)
}

Final Solution Link to heading

Putting all of this together we can derive y from o as follows:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

	y := o ^ (o >> _L)
	y = y ^ ((y << _T) & _C)
	mask := 0x7f
	for i := 0; i < 4; i ++ {
		b := _B & uint32(mask<<uint32(7*(uint32(i)+1)))
		y = y ^ ((y << _S) & b)
	}
	for i := 0; i < 3; i ++ {
		y = y ^ (y >> _U)
	}